投入产出分析学习笔记（一） 北师大讲座

Resource：https://www.bilibili.com/video/BV1tV411k7Mv?from=search&seid=6441224671028534611

1.基本概念

1.1来源

又称“部门平衡”分析，或称“产业联系”分析，最早由Leontief提出。主要通过编制投入产出表及建立相应的数学模型，反映经济系统各个部门（产业）之间的相互关系。

1.2应用

自20世纪60年代以来，投入产出分析被地理学家广泛应用于区域产业构成分析，区域相互作用分析，以及资源利用与环境保护研究等各个方面。是做区域变化、全球变化研究、碳排放问题等的利器！

1.3基本概念

• 投入：指一项经济活动中的各种消耗。包括物质和非物质产品消耗；有形和无形产品消耗。
• 产出：指生产活动的成果及分配使用去向、流向。（包括：物质和非物质产品、实物和服务产品）
• 投入产出表：指反映各种产品生产投入来源和分配去向的一种棋盘式表格。（矩阵表）
• 投入产出数学模型：指用数学模型（方程式）体现投入产出表所反映的经济内容的一组线性代数方程组。
• 作用：反映各部门、各产业生产与分配使用、生产与消耗之间的平衡关系。因此也称为部门联系平衡法。

2.投入产出模型基本原理

2.1模型分类

• 实物型投入产出表：以各种产品为对象，以不同的实物计量单位编制出来的；
• 价值型投入产出表：将整个经济系统划分为若干个子系统——生产部门，并以货币为计量单位。不仅能够反映各部门产品的实物运动过程，而且能够描述各部门产品的价值流动过程。

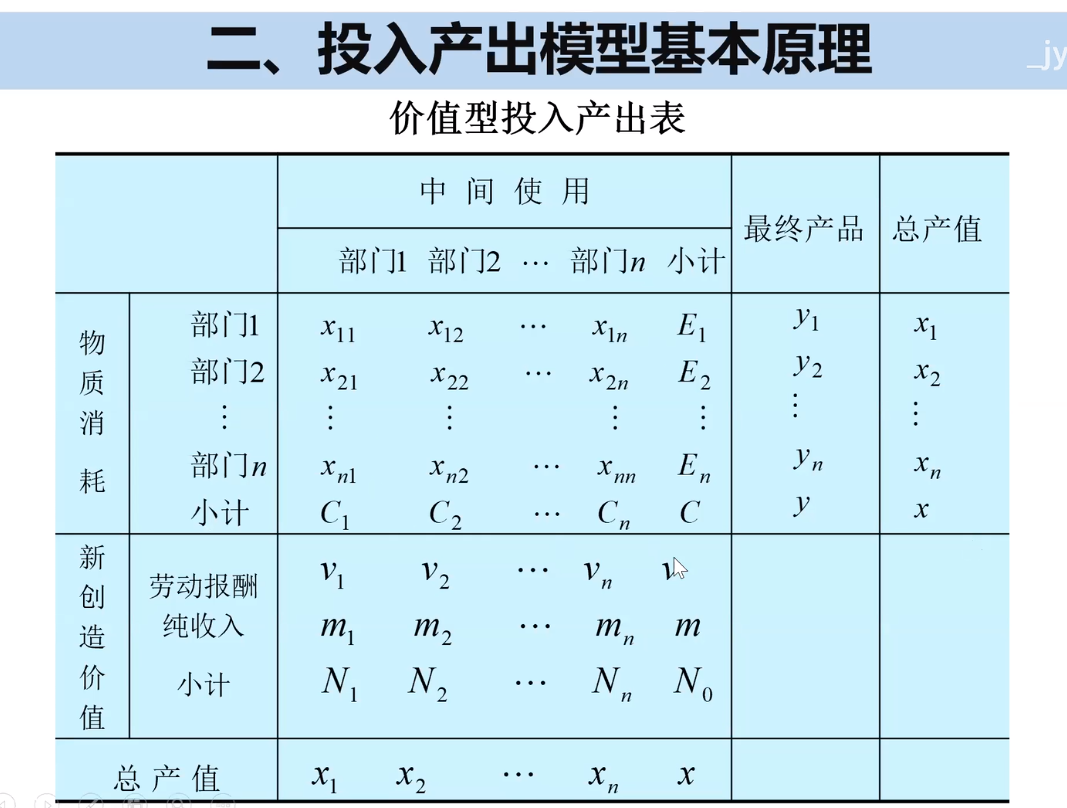
横向为产出、纵向为投入

假设部门1为农业，部门2为电力，则X₂₁的含义为，为满足农业部门的生产，电力部门的中间投入是多少；

E₁是为满足经济系统的中间使用，农业部门的总投入为多少；

C₁则为部门1所需要的的全部投入；

y₂表示电力部门的直接消耗总量；

x₁为第一行的加和，即E₁+y₁；

新创造价值即附加价值：

v₁即为农业部门的附加投入

• 行平衡关系：中间需求（Z）+ 最终使用（y）= 总产出（X）
• 列平衡关系：中间投入（Y）+ 增加值 （v）= 总投入（X）

直接消耗系数。核心方程，产品分配方程组

举个例子：

买一包泡面，Y就是个人对这包泡面的直接消费，但通过（I-A）^-1，可以追溯这包泡面的各项中间投入，如农业的小麦生产，工业中的外包装加工，运输投入、贸易等。

上图中，间接投入为一产品多次贸易的间接投入（系统）。L为Leontief逆矩阵。

按行建立模型较多。

3.环境扩展投入产出模型

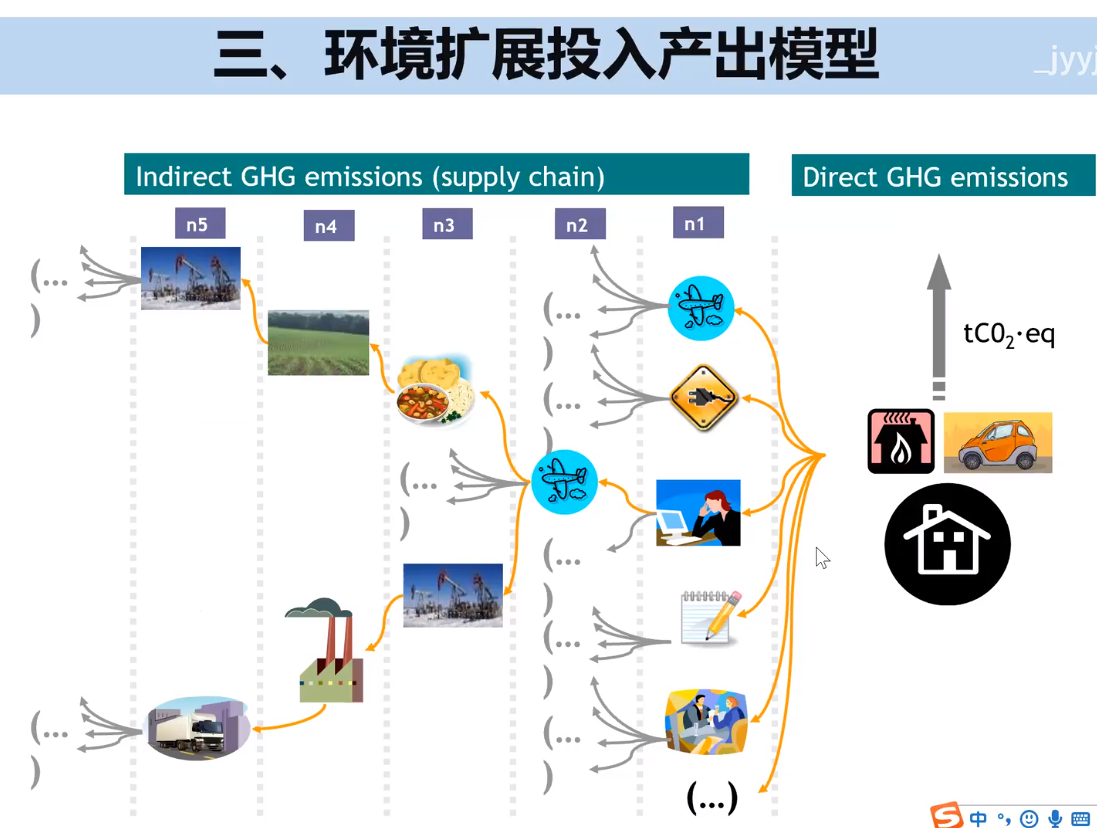
以碳排放为例，家庭取暖、燃烧等直接排放，电能、学习、社交等的间接碳排。（上图为学术交流中碳排放）

步长概念，如飞机，步长为2.

3.1作用与目的

• 对资源利用、环境排放问题的研究，通常忽视了资源利用、排放过程中各个产业部门之间的相互联系；
• 投入产出分析则是联系经济活动与环境污染和保护问题的一种行之有效的研究方法。在20世纪70年代初期，Leontief曾运用投入产出模型，对环境污染与治理问题作了研究。

3.2环境扩展的投入产出表

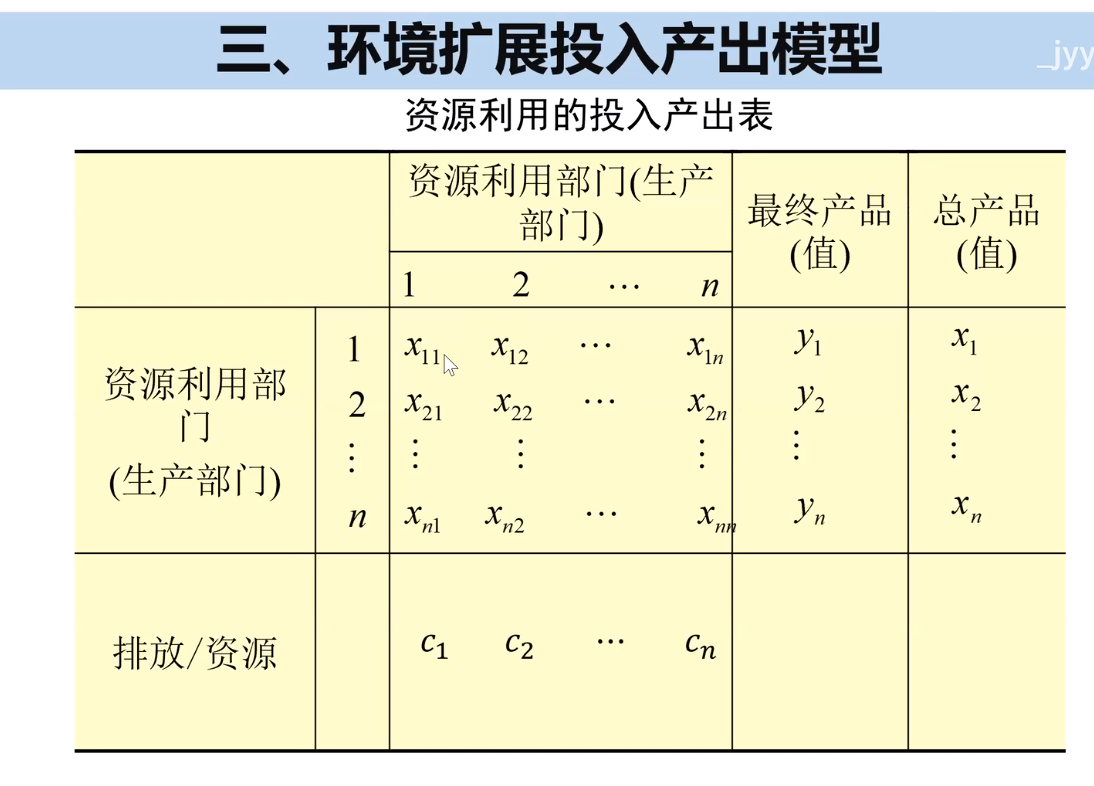
C₁为整个农业部门需要的资源消耗

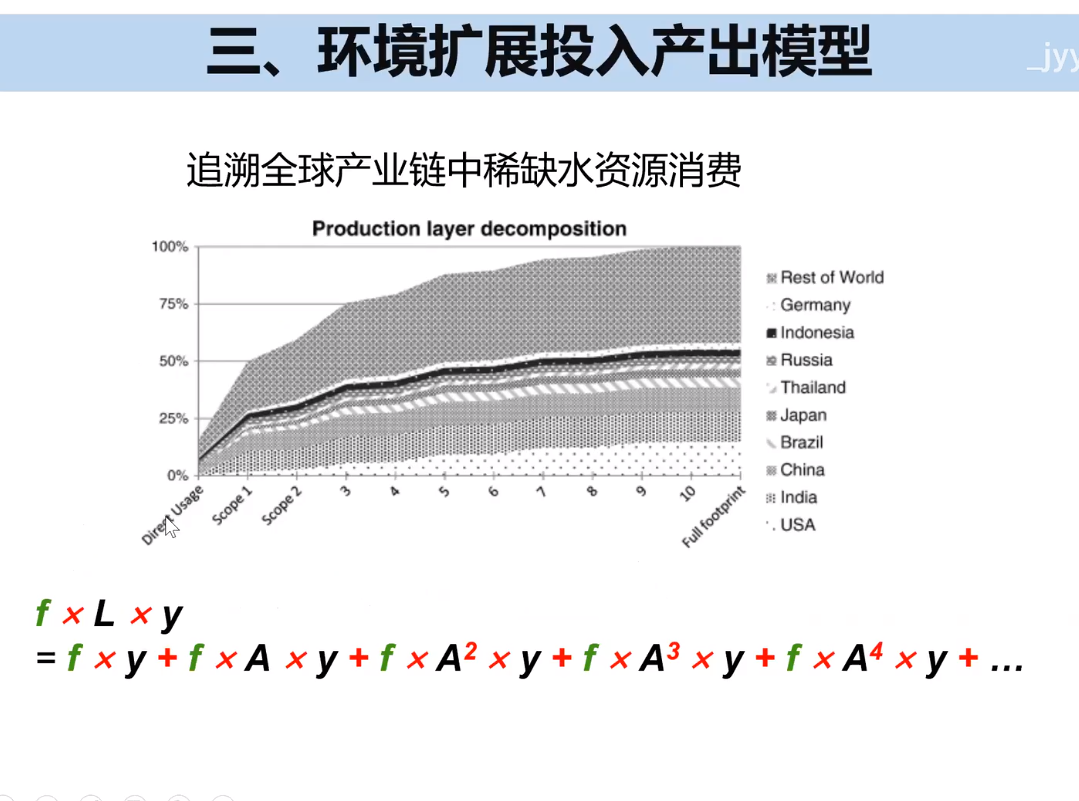
4.模型实际应用训练

呜呜呜，没有数据。

见excel